Detaillierte Analyse der RC -Serienschaltung
2024-05-08
20552
Die RC -Serienschaltung, die aus einem Widerstand und einem Kondensator besteht, dient sowohl als grundlegender Komponente in grundlegenden als auch in fortschrittlichen elektronischen Systemkonstruktionen.Es hilft, wichtige Prinzipien wie Frequenzgang, Phasenverschiebung und Signalfilterung zu verstehen, die eine wichtige Rolle bei der Schaltungsdesign und bei der Signalverarbeitung spielen.Diese Exploration deckt theoretische Grundlagen ab und erstreckt sich auf praktische Anwendungen durch Experimente und Simulationen.Durch physikalisches Zusammenbau der Schaltung oder das Modellieren digital können die Lernenden den Ladevorgang und die Auswirkungen von Komponenten v ariat -Ionen visuell erfassen und komplexe Konzepte zugänglicher und unvergesslicher machen.
Katalog

Abbildung 1: verschiedene Ausgangsspannungen von RC -Schaltungen
Einführung in die RC -Schaltung
Ein RC-Schaltkreis, kurz für den Widerstandskapazitätskreis, ist für die Elektronik von grundlegender Bedeutung, um Signale durch Widerstände und Kondensatoren zu manipulieren.Diese Schaltungen sind besonders bekannt für ihre Fähigkeit, Phasen zu verändern und Signale zu filtern, wobei einfache Anordnungen dieser Komponenten verwendet werden.Eine grundlegende RC-Schaltung, die häufig als RC-Schaltung erster Ordnung bezeichnet wird, umfasst normalerweise nur einen Widerstand und einen Kondensator.
In einem typischen Aufbau wird die Eingangsspannung auf die Serienanordnung eines Widerstands und eines Kondensators angewendet.Der Ausgang kann entweder über den Widerstand oder über den Kondensator gezogen werden, wobei jeweils aufgrund der einzigartigen Eigenschaften des Kondensators unterschiedliche Reaktionen auf Signalfrequenzen enthält.Diese Vielseitigkeit ermöglicht es RC -Schaltkreisen, eine Vielzahl von Rollen in elektronischen Geräten wie Kopplung und Filtersignale oder sogar Wellenformen zu konvertieren, wenn sie einer Schrittspannung ausgesetzt sind.
Die RC-Schaltung kann auf verschiedene Arten konfiguriert werden-Serien, parallel oder eine Kombination aus beiden, die als Serie-Parallel bezeichnet werden.Jede Konfiguration beeinflusst die Signalfrequenzen unterschiedlich: Serienverbindungen dämpfen tendenziell Niederfrequenzen, während parallele Verbindungen verwendet werden, um höhere Frequenzen zu dämpfen.Dieser Unterschied ist hauptsächlich auf die Art und Weise zurückzuführen, wie Widerstände und Kondensatoren mit der Schaltung interagieren.Widerstände sind direkt gegen den Strom, während die Kondensatoren ihn speichern und freigeben, und beeinflussen, wie die Schaltung auf unterschiedliche Frequenzen reagiert.
Im Gegensatz zu Schaltungen mit Induktoren wie LC -Schaltkreisen können einfache RC -Schaltkreise nicht Resonanz finden, da Widerstände keine Energie speichern.Dieses Attribut beeinflusst deutlich, wie RC -Schaltungen verwendet werden, und konzentriert sich auf ihre Fähigkeit zur Filterung und nicht auf Energiespeicher oder Resonanz.Jede Konfiguration dient zu einem bestimmten Zweck und macht RC -Schaltkreise sowohl in der theoretischen Untersuchung als auch in der praktischen Anwendung im elektronischen Design vielseitige Werkzeuge.
RC -Serienschaltung
Eine RC -Serienschaltung, im Wesentlichen aus einem Widerstand (bestehenR) und ein Kondensator (C) in Serie arbeitet nach einem einfachen Prinzip.Wenn der Schalter der Schaltung geschlossen ist, beginnt der Kondensator von der angelegten Spannung aufzuladen (V), initiieren einen Stromfluss durch die Schaltung.Wenn der Kondensator berechnet, steigt der Strom allmählich, bis der Kondensator seine Kapazität erreicht hat. An diesem Punkt wird die Annahme von Ladungen nicht mehr angenommen, und der Strom stabilisiert sich mit seinem Maximalwert, der als berechnet wird 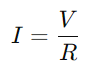 .
.
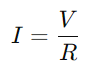 .
.Der Ladevorgang des Kondensators kann mathematisch durch die Gleichung beschrieben werden 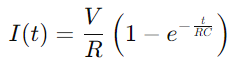 , wo ich der Strom ist, V ist die Spannung, R ist der Widerstand, C ist die Kapazität, T ist Zeit und e ist die Basis des natürlichen Logarithmus.Diese Formel spiegelt wider, wie sich der Strom im Laufe der Zeit ändert, wenn der Kondensator lädt, wobei das Produkt der Widerstands- und Kapazitätswerte (RC) die Zeitkonstante der Schaltung definiert, was auf die Geschwindigkeit hinweist, mit der der Kondensator lädt.
, wo ich der Strom ist, V ist die Spannung, R ist der Widerstand, C ist die Kapazität, T ist Zeit und e ist die Basis des natürlichen Logarithmus.Diese Formel spiegelt wider, wie sich der Strom im Laufe der Zeit ändert, wenn der Kondensator lädt, wobei das Produkt der Widerstands- und Kapazitätswerte (RC) die Zeitkonstante der Schaltung definiert, was auf die Geschwindigkeit hinweist, mit der der Kondensator lädt.
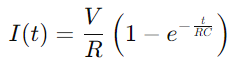 , wo ich der Strom ist, V ist die Spannung, R ist der Widerstand, C ist die Kapazität, T ist Zeit und e ist die Basis des natürlichen Logarithmus.Diese Formel spiegelt wider, wie sich der Strom im Laufe der Zeit ändert, wenn der Kondensator lädt, wobei das Produkt der Widerstands- und Kapazitätswerte (RC) die Zeitkonstante der Schaltung definiert, was auf die Geschwindigkeit hinweist, mit der der Kondensator lädt.
, wo ich der Strom ist, V ist die Spannung, R ist der Widerstand, C ist die Kapazität, T ist Zeit und e ist die Basis des natürlichen Logarithmus.Diese Formel spiegelt wider, wie sich der Strom im Laufe der Zeit ändert, wenn der Kondensator lädt, wobei das Produkt der Widerstands- und Kapazitätswerte (RC) die Zeitkonstante der Schaltung definiert, was auf die Geschwindigkeit hinweist, mit der der Kondensator lädt.
Abbildung 2: RC -Serienschaltung
Die Entladung tritt beim Öffnen des Schalters auf, wodurch der Prozess umgekehrt wird: Die gespeicherte Energie im Kondensator wird freigesetzt, wodurch der Strom in die entgegengesetzte Richtung fließt, bis der Kondensator entwässert wird.Dieser Lade- und Entlastungszyklus ist bei Anwendungen wie Signalumwandlung, Filterung und Zeitschaltungen von entscheidender Bedeutung, da sich der Strom und die Spannung ändern.

Abbildung 3: Kurzschluss der RC -Serie
Das Verhalten der RC -Serienschaltung variiert auch mit der Frequenz.Bei niedrigen Frequenzen wirkt der Kondensator eher wie ein offener Stromkreis und behindert den Stromfluss erheblich.Mit zunehmender Frequenz nimmt die kapazitive Reaktanz ab und erleichtert den Strom.Diese Änderung der Impedanz mit Frequenz ermöglicht es der RC -Serieschaltung, als Filter zu fungieren und die Frequenzen selektiv unter einem bestimmten Schwellenwert abzuschwächen (Drehfrequenz 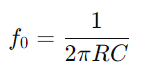 ).
).
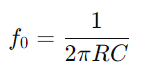 ).
).
Abbildung 4: Laden und Entladung von RC -Serienschaltungen
Zusätzlich zu stationären Vorgängen werden RC-Schaltungen auch für ihre transienten Antworten untersucht, wenn sie plötzliche Spannungsänderungen ausgesetzt werden, z.Dieses Szenario wird als vorübergehender Prozess bezeichnet, bei dem der Schaltkreis von einem stabilen Zustand in einen anderen übergeht.Die Dynamik dieses Prozesses hängt signifikant von der RC -Zeitkonstante ab, wodurch die Schaltung auf Änderungen reagiert.
Letztendlich erfüllen die RC -Serienschaltungen sowohl in DC- als auch in AC -Anwendungen mehrere Funktionen, wobei die Aufgaben von der Verzögerung von Signalen bis hin zur Integration oder Kopplung verschiedener Schaltungselemente reichen.Diese Vielseitigkeit beruht auf den einzigartigen Wechselwirkungen zwischen Widerstand und Kondensator, die zusammen die Gesamtreaktion der Schaltung auf Änderungen der Spannung und Frequenz bestimmen.

Abbildung 5: RC -Serienschaltungsdiagramm und Frequenzformel
In einer RC -Serie -Schaltung das Zusammenspiel zwischen dem Widerstand (R) und der Kondensator (C) beeinflusst sowohl den Stromfluss als auch die Spannungsverteilung.Die Hauptaufgabe des Widerstands besteht darin, den Stromfluss zu regulieren.Diese Beziehung wird nach dem Ohmschen Gesetz quantifiziert, das heißt 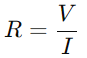 , Wo V ist Spannung und ICH ist aktuell.Im Wesentlichen fungiert der Widerstand als Engpass und kontrolliert, wie viel Strom zu einem bestimmten Zeitpunkt durchlaufen kann.
, Wo V ist Spannung und ICH ist aktuell.Im Wesentlichen fungiert der Widerstand als Engpass und kontrolliert, wie viel Strom zu einem bestimmten Zeitpunkt durchlaufen kann.
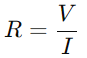 , Wo V ist Spannung und ICH ist aktuell.Im Wesentlichen fungiert der Widerstand als Engpass und kontrolliert, wie viel Strom zu einem bestimmten Zeitpunkt durchlaufen kann.
, Wo V ist Spannung und ICH ist aktuell.Im Wesentlichen fungiert der Widerstand als Engpass und kontrolliert, wie viel Strom zu einem bestimmten Zeitpunkt durchlaufen kann.Die Funktion des Kondensators ist etwas komplizierter, da sie die elektrische Energie vorübergehend gespeichert und dann wieder in den Schaltkreis füllt.Die Spannung über den Kondensator (VC) korreliert mit seiner gespeicherten Ladung (Q) und wird unter Verwendung der Formel berechnet 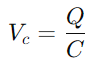 .Diese Beziehung unterstreicht die Kapazität des Kondensators, die die Ladung zu halten, und wirkt sich direkt auf die Spannung aus, die sie aufweist.Während des Betriebs ist die Dynamik des Aufladens und der Entlassung des Kondensators für das Verständnis von RC -Schaltungen von entscheidender Bedeutung.Die Zeitkonstante (τ), definiert als
.Diese Beziehung unterstreicht die Kapazität des Kondensators, die die Ladung zu halten, und wirkt sich direkt auf die Spannung aus, die sie aufweist.Während des Betriebs ist die Dynamik des Aufladens und der Entlassung des Kondensators für das Verständnis von RC -Schaltungen von entscheidender Bedeutung.Die Zeitkonstante (τ), definiert als 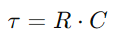 , misst, wie schnell der Kondensator ungefähr 63,2% der von der Quelle gelieferten Vollspannung erreicht (Quelle (V0).Diese Zeitkonstante zeigt, wie sich die Schaltung an Eingangsänderungen anpasst, wobei die Eigenschaften des Widerstands und der Kondensator das Tempo dieser Anpassungen diktieren.
, misst, wie schnell der Kondensator ungefähr 63,2% der von der Quelle gelieferten Vollspannung erreicht (Quelle (V0).Diese Zeitkonstante zeigt, wie sich die Schaltung an Eingangsänderungen anpasst, wobei die Eigenschaften des Widerstands und der Kondensator das Tempo dieser Anpassungen diktieren.
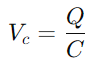 .Diese Beziehung unterstreicht die Kapazität des Kondensators, die die Ladung zu halten, und wirkt sich direkt auf die Spannung aus, die sie aufweist.Während des Betriebs ist die Dynamik des Aufladens und der Entlassung des Kondensators für das Verständnis von RC -Schaltungen von entscheidender Bedeutung.Die Zeitkonstante (τ), definiert als
.Diese Beziehung unterstreicht die Kapazität des Kondensators, die die Ladung zu halten, und wirkt sich direkt auf die Spannung aus, die sie aufweist.Während des Betriebs ist die Dynamik des Aufladens und der Entlassung des Kondensators für das Verständnis von RC -Schaltungen von entscheidender Bedeutung.Die Zeitkonstante (τ), definiert als 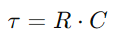 , misst, wie schnell der Kondensator ungefähr 63,2% der von der Quelle gelieferten Vollspannung erreicht (Quelle (V0).Diese Zeitkonstante zeigt, wie sich die Schaltung an Eingangsänderungen anpasst, wobei die Eigenschaften des Widerstands und der Kondensator das Tempo dieser Anpassungen diktieren.
, misst, wie schnell der Kondensator ungefähr 63,2% der von der Quelle gelieferten Vollspannung erreicht (Quelle (V0).Diese Zeitkonstante zeigt, wie sich die Schaltung an Eingangsänderungen anpasst, wobei die Eigenschaften des Widerstands und der Kondensator das Tempo dieser Anpassungen diktieren.Die Spannung über den Kondensator zu jedem Zeitpunkt während der Ladung ist gegeben von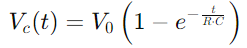 Veranschaulichung eines nichtlinearen Anstiegs beim Ausfüllen des Kondensators.Diese Gleichung beschreibt, wie sich die Ladungsrate verlangsamt, wenn sich der Kondensator der vollen Kapazität nähert.
Veranschaulichung eines nichtlinearen Anstiegs beim Ausfüllen des Kondensators.Diese Gleichung beschreibt, wie sich die Ladungsrate verlangsamt, wenn sich der Kondensator der vollen Kapazität nähert.
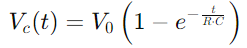 Veranschaulichung eines nichtlinearen Anstiegs beim Ausfüllen des Kondensators.Diese Gleichung beschreibt, wie sich die Ladungsrate verlangsamt, wenn sich der Kondensator der vollen Kapazität nähert.
Veranschaulichung eines nichtlinearen Anstiegs beim Ausfüllen des Kondensators.Diese Gleichung beschreibt, wie sich die Ladungsrate verlangsamt, wenn sich der Kondensator der vollen Kapazität nähert.Umgekehrt nimmt die Spannungsspannung des Kondensators nach Entladung nach 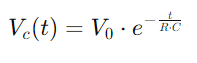 Darstellung einer linearen Abnahme der gespeicherten Energie im Laufe der Zeit.Dieser Prozess liefert ein klares Bild davon, wie Energie vom Kondensator zurück in die Schaltung freigesetzt wird.In AC -Anwendungen der Phasenunterschied zwischen Spannung und Strom, φ, wird kritisch.Dieser Unterschied, berechnet als
Darstellung einer linearen Abnahme der gespeicherten Energie im Laufe der Zeit.Dieser Prozess liefert ein klares Bild davon, wie Energie vom Kondensator zurück in die Schaltung freigesetzt wird.In AC -Anwendungen der Phasenunterschied zwischen Spannung und Strom, φ, wird kritisch.Dieser Unterschied, berechnet als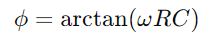 Wo ω Repräsentiert die Winkelfrequenz, zeigt die durch den Kondensator verursachte Verzögerung, die den Zeitpunkt zwischen den Stromflüssen und Spannungsänderungen über die Komponenten beeinflusst.
Wo ω Repräsentiert die Winkelfrequenz, zeigt die durch den Kondensator verursachte Verzögerung, die den Zeitpunkt zwischen den Stromflüssen und Spannungsänderungen über die Komponenten beeinflusst.
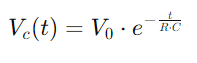 Darstellung einer linearen Abnahme der gespeicherten Energie im Laufe der Zeit.Dieser Prozess liefert ein klares Bild davon, wie Energie vom Kondensator zurück in die Schaltung freigesetzt wird.In AC -Anwendungen der Phasenunterschied zwischen Spannung und Strom, φ, wird kritisch.Dieser Unterschied, berechnet als
Darstellung einer linearen Abnahme der gespeicherten Energie im Laufe der Zeit.Dieser Prozess liefert ein klares Bild davon, wie Energie vom Kondensator zurück in die Schaltung freigesetzt wird.In AC -Anwendungen der Phasenunterschied zwischen Spannung und Strom, φ, wird kritisch.Dieser Unterschied, berechnet als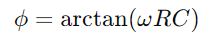 Wo ω Repräsentiert die Winkelfrequenz, zeigt die durch den Kondensator verursachte Verzögerung, die den Zeitpunkt zwischen den Stromflüssen und Spannungsänderungen über die Komponenten beeinflusst.
Wo ω Repräsentiert die Winkelfrequenz, zeigt die durch den Kondensator verursachte Verzögerung, die den Zeitpunkt zwischen den Stromflüssen und Spannungsänderungen über die Komponenten beeinflusst.Insgesamt begrenzt der Widerstand und leitet den Stromfluss, während der Kondensator die Spannung speichert und moduliert.Zusammen bestimmen sie die Reaktionsmerkmale der Schaltung, z.Dieses kombinierte Verhalten untermauert die grundlegenden Operationen von RC -Serienschaltungen, wodurch sie in verschiedenen elektronischen Anwendungen integriert werden.
Grundgleichungen der RC -Serienschaltung
Um das Verhalten einer RC -Serienschaltung zu verstehen, ist es wichtig, mit den grundlegenden Gleichungen zu beginnen, die seine Reaktion auf Änderungen der Eingangsspannung beschreiben.Angenommen, wir haben eine sich ändernde Eingangsspannung als als Vin (t)mit der Spannung über den Widerstand als als markiert als als Vr (t) und über den Kondensator als VC (t).In einer Serienschaltung der gleiche Strom, Es) fließt sowohl durch den Widerstand als auch durch den Kondensator.
Wenn Sie Kirchhoffs Spannungsgesetz (KVL) anwenden, in dem die Gesamtspannung um jede geschlossene Schleife in einer Schaltung gleich Null sein muss, stellen wir fest, dass die Eingangsspannung der Summe der Spannungen über den Widerstand und den Kondensator entspricht:

Die Spannung über den Widerstand kann nach dem Ohmschen Gesetz berechnet werden:
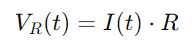
Für den Kondensator ist der Spannungs -VC (t) mit der Ladung q (t) in Verbindung gebracht, die sie gilt, gegeben durch:
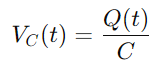
Da der Strom als die Rate des Ladungsflusss definiert ist, haben wir:
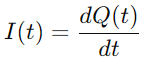
Durch Ersetzen Q (t) in der Gleichung für VC (t)und Verwendung des Ladungsabgangs Es)Wir leiten die Kerndifferentialgleichung für den RC -Serienkreis ab:

Weiter ersetzen Q (t) mit dem Integral von Es), wir bekommen:
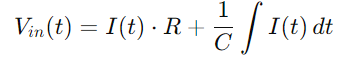
Für den Strom I (T) verwenden wir unter Berücksichtigung der Spannungsänderung der Spannung über den Kondensator:
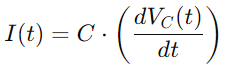
Durch die Integration all dieser Beziehungen gibt wir die Differentialgleichung, die die Spannung über den Kondensator beschreibt:
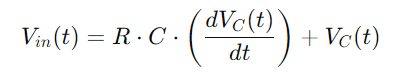
Dies ist eine lineare Differentialgleichung erster Ordnung, die die zeitabhängige Änderung der Spannung über den Kondensator erfasst.Durch die Lösung dieser Gleichung können wir genau beschreiben, wie sich die Kondensatorspannung entwickelt.Dieses Verständnis ist grundlegend für die Analyse sowohl der Lade- als auch der Entladungszyklen des Kondensators sowie der Reaktion der Schaltung auf verschiedene Frequenzen.Dieser umfassende Ansatz liefert einen tiefen Einblick in die dynamischen Eigenschaften der RC -Serienschaltung.

Abbildung 6: Spannungsdifferenzgleichung
Impedanz der RC -Serienschaltung
Um die Beschreibung einer RC-Serie-Schaltung mit Schwerpunkt auf menschlicher Interaktion und einer direkten, vereinfachten Erklärung umzuschreiben, verbessern wir die materiellen Erfahrungen und schrittweisen Vorgänge, während die Kernbotschaft und Kohärenz beibehalten werden:
In einer RC -Serie -Schaltung arbeiten der Widerstand und der Kondensator zusammen, um den Stromfluss zu steuern, was bei der Bearbeitung von Wechselströmen von entscheidender Bedeutung ist.Die Gesamtimpedanz der Schaltung, dargestellt als 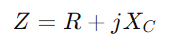 kombiniert den Widerstand R und die kapazitive Reaktanz XC.Das Schlüsselmerkmal dieses Setups ist, dass die Impedanzwerte für beide Komponenten mit Frequenzänderungen variieren.Wenn die Frequenz zunimmt, nimmt die Impedanz des Kondensators ab und lässt mehr Strom durchlaufen, während der Widerstand im Wesentlichen konstant bleibt.
kombiniert den Widerstand R und die kapazitive Reaktanz XC.Das Schlüsselmerkmal dieses Setups ist, dass die Impedanzwerte für beide Komponenten mit Frequenzänderungen variieren.Wenn die Frequenz zunimmt, nimmt die Impedanz des Kondensators ab und lässt mehr Strom durchlaufen, während der Widerstand im Wesentlichen konstant bleibt.
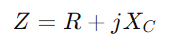 kombiniert den Widerstand R und die kapazitive Reaktanz XC.Das Schlüsselmerkmal dieses Setups ist, dass die Impedanzwerte für beide Komponenten mit Frequenzänderungen variieren.Wenn die Frequenz zunimmt, nimmt die Impedanz des Kondensators ab und lässt mehr Strom durchlaufen, während der Widerstand im Wesentlichen konstant bleibt.
kombiniert den Widerstand R und die kapazitive Reaktanz XC.Das Schlüsselmerkmal dieses Setups ist, dass die Impedanzwerte für beide Komponenten mit Frequenzänderungen variieren.Wenn die Frequenz zunimmt, nimmt die Impedanz des Kondensators ab und lässt mehr Strom durchlaufen, während der Widerstand im Wesentlichen konstant bleibt.Die Impedanz, bezeichnet als als Z und in Ohm (ω) gemessen, spielt eine entscheidende Rolle bei der Bestimmung, wie der Schaltkreis auf abwechselnden Strom reagiert.Wie in RL Series Circuits der Widerstand R und kapazitive Reaktanz xC einer RC -Schaltung bilden ein Dreieck, das als Impedanzdreieck bekannt ist.Dieses Dreieck bezieht sich eng mit dem Spannungsdreieck. Durch die Anwendung des pythagoräischen Theorems können Sie die Gesamtimpedanz der Schaltung berechnen.

Abbildung 7: RC -Serie -Schaltungsberechnung Formel
Betrachten Sie bei praktischen Anwendungen Kopfhörer, die diese Prinzipien verwenden.Hochleistungs-Kopfhörer mit mehr als 200 Ohm werden typischerweise mit Desktop-Computern, Stromverstärkern und professionellen Audiogeräten verwendet.Diese hochwertigen Modelle übereinstimmen gut zu den Ausgangsfunktionen der professionellen Elektronik.Bei Verwendung dieser Kopfhörer ist es entscheidend, das Volumen allmählich anzupassen, um Überladung und Beschädigung der empfindlichen internen Komponenten wie der Sprachspule zu vermeiden.
Umgekehrt werden Kopfhörer mit niedrigen Impedanz, normalerweise unter 50 Ohm, für tragbare Geräte wie CD-Player, MD-Player oder MP3-Player bevorzugt.Diese Kopfhörer erfordern weniger Strom, um hochwertige Audio zu liefern, was sie ideal für den mobilen Gebrauch macht.Sie erfordern jedoch auch sorgfältige Aufmerksamkeit auf die Sensitivitätsniveaus, um eine optimale Leistung zu gewährleisten und Schäden an Kopfhörern oder Hören zu verhindern.

Abbildung 8: Impedanzdiagramm der RC -Serieschaltung
Zulassungs- und Analyseverfahren von RC -Serienschaltungen
Die Zulassung misst, wie leicht ein RC -Serienschaltungsschaltung Strom leisten kann, berechnet als Umkehrung der Impedanz (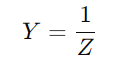 ).Dieser Wert integriert beide den Widerstand (R) und die Reaktanz (X) der Schaltung.Der Widerstand widerspricht dem Stromfluss, indem sie die elektrische Energie in Wärme umwandelt, während Reaktanz Energie vorübergehend in der Schaltung speichert.
).Dieser Wert integriert beide den Widerstand (R) und die Reaktanz (X) der Schaltung.Der Widerstand widerspricht dem Stromfluss, indem sie die elektrische Energie in Wärme umwandelt, während Reaktanz Energie vorübergehend in der Schaltung speichert.
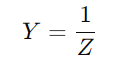 ).Dieser Wert integriert beide den Widerstand (R) und die Reaktanz (X) der Schaltung.Der Widerstand widerspricht dem Stromfluss, indem sie die elektrische Energie in Wärme umwandelt, während Reaktanz Energie vorübergehend in der Schaltung speichert.
).Dieser Wert integriert beide den Widerstand (R) und die Reaktanz (X) der Schaltung.Der Widerstand widerspricht dem Stromfluss, indem sie die elektrische Energie in Wärme umwandelt, während Reaktanz Energie vorübergehend in der Schaltung speichert.Zulassung berechnen
Beginnen Sie mit dem Schreiben der Impedanz 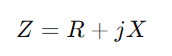 , wo r für Widerstand steht, X zur Reaktanz und J ist die imaginäre Einheit.Verwenden Sie die Formel y = 1/((R + JX).Diese Operation beinhaltet komplexe Zahlen und gibt uns
, wo r für Widerstand steht, X zur Reaktanz und J ist die imaginäre Einheit.Verwenden Sie die Formel y = 1/((R + JX).Diese Operation beinhaltet komplexe Zahlen und gibt uns 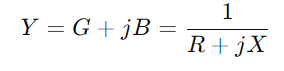 .Hier, G ist die Leitfähigkeit (tatsächliche Stromflussfähigkeit) und B ist die Anfälligkeit (die Fähigkeit der Schaltung, auf Änderungen des Stroms zu reagieren).
.Hier, G ist die Leitfähigkeit (tatsächliche Stromflussfähigkeit) und B ist die Anfälligkeit (die Fähigkeit der Schaltung, auf Änderungen des Stroms zu reagieren).
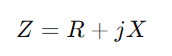 , wo r für Widerstand steht, X zur Reaktanz und J ist die imaginäre Einheit.Verwenden Sie die Formel y = 1/((R + JX).Diese Operation beinhaltet komplexe Zahlen und gibt uns
, wo r für Widerstand steht, X zur Reaktanz und J ist die imaginäre Einheit.Verwenden Sie die Formel y = 1/((R + JX).Diese Operation beinhaltet komplexe Zahlen und gibt uns 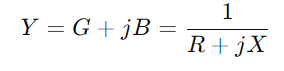 .Hier, G ist die Leitfähigkeit (tatsächliche Stromflussfähigkeit) und B ist die Anfälligkeit (die Fähigkeit der Schaltung, auf Änderungen des Stroms zu reagieren).
.Hier, G ist die Leitfähigkeit (tatsächliche Stromflussfähigkeit) und B ist die Anfälligkeit (die Fähigkeit der Schaltung, auf Änderungen des Stroms zu reagieren).
Abbildung 9: Serie RC -Schaltungsimpedanzrechner
Diese Berechnung zeigt nicht nur die Leitfähigkeit der Schaltung, sondern auch die dynamischen Reaktionseigenschaften, was für die Analyse der Wechselstromkreis entscheidend ist.Leitfähigkeit und Anfälligkeit, zusammengenommen, geben Sie an, wie die Schaltung Strom übergeht und wie sie Energie speichert und freigibt.

Abbildung 10: Phasenwinkelformel
Praktische Anwendung
Ingenieure verwenden Zulassungswerte, um das Schaltungsdesign zu verbessern, insbesondere in hochfrequenten Anwendungen wie Funkfrequenzschaltungen.Die Anpassung der Zulassung hilft bei der Impedanzanpassung, zur Verringerung der Signalreflexion und zur Steigerung der Übertragungseffizienz.
Durch die Untersuchung der Zulassungsreaktion können die Ingenieure die Leistungsleistung unter verschiedenen Bedingungen wie Frequenzgang, Stabilität und Empfindlichkeit bewerten und vorhersagen.Mit einem Oszilloskop und einem Signalgenerator ausrüsten, um die Spannung und den Strom der Schaltung bei unterschiedlichen Frequenzen zu messen.Konzentrieren Sie sich insbesondere auf die Grenzfrequenz, um theoretische Vorhersagen zu testen und sie gegen praktische Beobachtungen zu validieren.Beginnen Sie für AC -Schaltungen mit der Bestimmung der Reaktanz (XC) des Kondensators mit 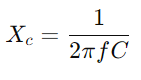 , Wo F ist die Signalfrequenz.Berechnen Sie die Gesamtimpedanz
, Wo F ist die Signalfrequenz.Berechnen Sie die Gesamtimpedanz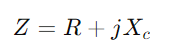 und dann Zulassung
und dann Zulassung 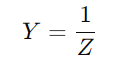 .
.
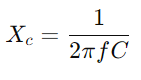 , Wo F ist die Signalfrequenz.Berechnen Sie die Gesamtimpedanz
, Wo F ist die Signalfrequenz.Berechnen Sie die Gesamtimpedanz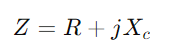 und dann Zulassung
und dann Zulassung 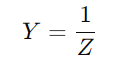 .
.Phasenunterschied analysieren 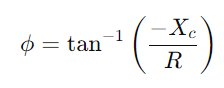 Veränderung der Signalform zu verstehen.Untersuchen
Veränderung der Signalform zu verstehen.Untersuchen 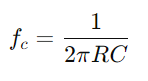 , wo der Schaltkreis vom Übergang zu Blocksignalen verschiebt.Die Bewertung, wie Impedanz und Phasenunterschiede mit der Frequenz variieren, ist entscheidend für die Gestaltung effektiver Filter und Signalprozessoren.Besprechen Sie, wie Frequenzselektivität, Phasenverschiebungen und Signalschwächung aufgrund der Eigenschaften des Schaltungskreises praktische Anwendungen wie Filterung und elektronisches Tuning beeinflussen.
, wo der Schaltkreis vom Übergang zu Blocksignalen verschiebt.Die Bewertung, wie Impedanz und Phasenunterschiede mit der Frequenz variieren, ist entscheidend für die Gestaltung effektiver Filter und Signalprozessoren.Besprechen Sie, wie Frequenzselektivität, Phasenverschiebungen und Signalschwächung aufgrund der Eigenschaften des Schaltungskreises praktische Anwendungen wie Filterung und elektronisches Tuning beeinflussen.
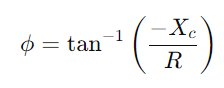 Veränderung der Signalform zu verstehen.Untersuchen
Veränderung der Signalform zu verstehen.Untersuchen 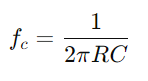 , wo der Schaltkreis vom Übergang zu Blocksignalen verschiebt.Die Bewertung, wie Impedanz und Phasenunterschiede mit der Frequenz variieren, ist entscheidend für die Gestaltung effektiver Filter und Signalprozessoren.Besprechen Sie, wie Frequenzselektivität, Phasenverschiebungen und Signalschwächung aufgrund der Eigenschaften des Schaltungskreises praktische Anwendungen wie Filterung und elektronisches Tuning beeinflussen.
, wo der Schaltkreis vom Übergang zu Blocksignalen verschiebt.Die Bewertung, wie Impedanz und Phasenunterschiede mit der Frequenz variieren, ist entscheidend für die Gestaltung effektiver Filter und Signalprozessoren.Besprechen Sie, wie Frequenzselektivität, Phasenverschiebungen und Signalschwächung aufgrund der Eigenschaften des Schaltungskreises praktische Anwendungen wie Filterung und elektronisches Tuning beeinflussen.Dieser Ansatz unterteilt die operativen Prozesse in überschaubare Schritte und bereichert das Verständnis des Benutzers mit praktischen Einsichten in die Handhabung und Analyse von RC -Serienschaltungen.

Abbildung 11: Eigenschaften der RC -Serienschaltungen
Phasordiagramm der RC -Serieschaltung
In einer RC -Serienschaltung teilen sich alle Elemente aufgrund ihrer Serienkonfiguration den gleichen Strom.Dieser gleichmäßige Strom wirkt als Grundlinie für unser Phasordiagramm, mit dem die Beziehung zwischen verschiedenen Spannungen und Strömen in der Schaltung visualisiert wird.Lassen Sie uns diesen Strom bezeichnen ICH als Referenzphasor, positioniert bei null Grad auf dem Diagramm.Im Diagramm der Strom ICH ist horizontal nach rechts eingestellt und erstellt die Referenzlinie mit Null-Grad.Die Spannung über den Widerstand (UR) ist in Phase mit dem Strom, da Widerstände keine Phasenverschiebung verursachen.Daher, UR wird als horizontaler Vektor in die gleiche Richtung wie gezeichnet wie ICHsich vom Ursprung erstrecken.

Abbildung 12: Phasordiagramm der RC Series Circuit
Im Gegensatz dazu die Spannung über den Kondensator (UC) führt den Strom aufgrund der kapazitiven Eigenschaft der Verzögerung der Stromphase um 90 Grad.Diese Spannung wird durch einen vertikalen Vektor dargestellt, der nach oben zeigt, beginnend mit der Spitze der UR Vektor.Die Gesamtspannung U In der Schaltung ist die Vektorsumme von U Rand UC.Diese Summe bildet ein rechtes Dreieck mit UR Und UC als angrenzende bzw. entgegengesetzte Seiten.Die Hypotenuse dieses Dreiecks, die sich vom Ursprung bis zur Spitze der Spitze erstreckt UC Vektor, repräsentiert U.
Der sinusförmige Strom durch die Schaltung wird durch die Sünde gegeben (ωt), wo IM die maximale Stromamplitude ist und ω ist die Winkelfrequenz.Folglich ist die Spannung über den Widerstand 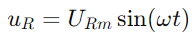 , spiegeln die Stromwellenform wider.Die Spannung über den Kondensator ist gegeben durch
, spiegeln die Stromwellenform wider.Die Spannung über den Kondensator ist gegeben durch 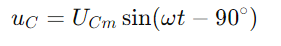 , Angabe einer Phasenverschiebung von –90 ° (oder 90 Grad vor dem Strom).Das rechte Dreieck des Phasordiagramms verdeutlicht das
, Angabe einer Phasenverschiebung von –90 ° (oder 90 Grad vor dem Strom).Das rechte Dreieck des Phasordiagramms verdeutlicht das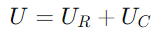 ist nicht nur in der Größe, sondern auch in Phasenbeziehung mit dem Anschlussspannungsvektor (U) Abschluss des Dreiecks.
ist nicht nur in der Größe, sondern auch in Phasenbeziehung mit dem Anschlussspannungsvektor (U) Abschluss des Dreiecks.
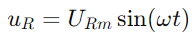 , spiegeln die Stromwellenform wider.Die Spannung über den Kondensator ist gegeben durch
, spiegeln die Stromwellenform wider.Die Spannung über den Kondensator ist gegeben durch 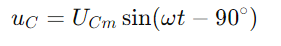 , Angabe einer Phasenverschiebung von –90 ° (oder 90 Grad vor dem Strom).Das rechte Dreieck des Phasordiagramms verdeutlicht das
, Angabe einer Phasenverschiebung von –90 ° (oder 90 Grad vor dem Strom).Das rechte Dreieck des Phasordiagramms verdeutlicht das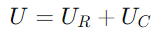 ist nicht nur in der Größe, sondern auch in Phasenbeziehung mit dem Anschlussspannungsvektor (U) Abschluss des Dreiecks.
ist nicht nur in der Größe, sondern auch in Phasenbeziehung mit dem Anschlussspannungsvektor (U) Abschluss des Dreiecks.
Abbildung 13: Spannungsphasordiagramm der RC -Serieschaltung
Schlüsselpunkte bei der Analyse der RC -Schaltungen der Serie RC
Impedanz in der Serie RC -Schaltung, dargestellt als Z, kombiniert Widerstand (R) und die reaktive Wirkung der Kapazität in ein einzelnes Maß, das mit der Signalfrequenz variiert.Es wird mathematisch ausgedrückt als 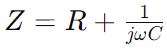 , Wo ω ist die Winkelfrequenz und C ist die Kapazität.Hier, R stellt den eigentlichen Teil der Impedanz dar und
, Wo ω ist die Winkelfrequenz und C ist die Kapazität.Hier, R stellt den eigentlichen Teil der Impedanz dar und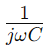 repräsentiert den imaginären Teil und zeigt an, wie der Kondensator die Schaltung beeinflusst.
repräsentiert den imaginären Teil und zeigt an, wie der Kondensator die Schaltung beeinflusst.
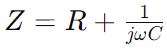 , Wo ω ist die Winkelfrequenz und C ist die Kapazität.Hier, R stellt den eigentlichen Teil der Impedanz dar und
, Wo ω ist die Winkelfrequenz und C ist die Kapazität.Hier, R stellt den eigentlichen Teil der Impedanz dar und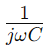 repräsentiert den imaginären Teil und zeigt an, wie der Kondensator die Schaltung beeinflusst.
repräsentiert den imaginären Teil und zeigt an, wie der Kondensator die Schaltung beeinflusst.Die Art und Weise, wie die Impedanz mit Frequenz ändert, ist für die Verwendung von RC -Schaltungen der Serie RC in Filteranwendungen entscheidend.Bei niedrigeren Frequenzen weist die Schaltung eine höhere Impedanz auf und blockiert diese Frequenzen effektiv.Umgekehrt sinkt die Impedanz bei höheren Frequenzen, sodass diese Frequenzen freier gehen können.Dieses Verhalten macht Serien RC-Schaltkreise ideal für Aufgaben wie das Filtern unerwünschter Niederfrequenzrauschen oder das Bestehen von Hochfrequenzsignalen.

Abbildung 14: Impedanzvektordiagramm der RC -Serieschaltung
Abschluss
Von der Filterung unerwünschter Frequenzen bis hin zur Gestaltung der Signalreaktionen ist die RC -Serieschaltung in einem breiten Bereich elektronischer Funktionen maßgeblich beteiligt.Durch das Verständnis der zugrunde liegenden Prinzipien wie Impedanz, Phasorbeziehungen und des frequenzabhängigen Verhaltens dieser Schaltkreise sind Ingenieure und Designer für die Erstellung von Lösungen gerüstet, die die Signalintegrität in komplexen elektronischen Systemen effektiv verwalten.Die detaillierte Untersuchung dieser Schaltkreise, unterstützt durch mathematische Analysen und visuelle Darstellungen wie Phasordiagramme, bietet einen umfassenden Einblick, der für alle wichtig ist, die ihr Verständnis der Dynamik der elektronischen Schaltung vertiefen oder ihre praktischen Fähigkeiten in der Schaltungsdesign und der Fehlerbehebung verbessern möchten.
Häufig gestellte Fragen [FAQ]
1. Was ist das Prinzip der RC -Schaltung?
Das Prinzip eines RC-Schaltkreises (Widerstandskapazitor) dreht sich um die Lade- und Entladungsprozesse des Kondensators durch den Widerstand.In dieser Schaltung interagiert die Fähigkeit des Kondensators, elektrische Energie zu speichern und freizusetzen, mit dem Widerstand, der die Geschwindigkeit steuert, mit der der Kondensator lädt oder entlassen.
2. Warum führt ein RC -Schaltungsstrom?
In einem RC -Schaltkreis führt der Strom die Spannung über den Kondensator, da der Kondensator mit dem Aufladen beginnen muss, bevor seine Spannung steigen kann.Da der Strom in den Kondensator fließt, um ihn zu laden, erreicht der Strom vor der Spannung über den Kondensator sein Maximum.Dieser Effekt bewirkt eine Phasenverschiebung, bei der die Stromphase die Spannungsphase je nach Frequenz des Eingangssignals bis zu 90 Grad führt.
3. Wie ändert sich die Spannung in einer RC -Schaltung?
Die Spannungsänderung in einem RC -Schaltkreis während des Ladens wird durch eine exponentielle Funktion beschrieben.Wenn eine Spannung angewendet wird, nimmt die Spannung über den Kondensator zunächst schnell zu und verlangsamt sich dann, wenn sie sich der Versorgungsspannung nähert.Mathematisch wird dies als ausgedrückt als 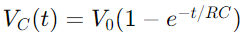 , Wo VC(T) ist die Spannung über den Kondensator zum Zeitpunkt t, V0 ist die Versorgungsspannung und RC ist die Zeitkonstante der Schaltung, die feststellt, wie schnell der Kondensator berechnet.Umgekehrt nimmt die Spannung während des Entladens über den Kondensator exponentiell nach der Gleichung ab
, Wo VC(T) ist die Spannung über den Kondensator zum Zeitpunkt t, V0 ist die Versorgungsspannung und RC ist die Zeitkonstante der Schaltung, die feststellt, wie schnell der Kondensator berechnet.Umgekehrt nimmt die Spannung während des Entladens über den Kondensator exponentiell nach der Gleichung ab 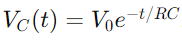 .
.
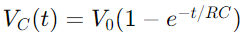 , Wo VC(T) ist die Spannung über den Kondensator zum Zeitpunkt t, V0 ist die Versorgungsspannung und RC ist die Zeitkonstante der Schaltung, die feststellt, wie schnell der Kondensator berechnet.Umgekehrt nimmt die Spannung während des Entladens über den Kondensator exponentiell nach der Gleichung ab
, Wo VC(T) ist die Spannung über den Kondensator zum Zeitpunkt t, V0 ist die Versorgungsspannung und RC ist die Zeitkonstante der Schaltung, die feststellt, wie schnell der Kondensator berechnet.Umgekehrt nimmt die Spannung während des Entladens über den Kondensator exponentiell nach der Gleichung ab 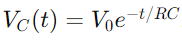 .
. ÜBER UNS
Kundenzufriedenheit jedes Mal.Gegenseitiges Vertrauen und gemeinsame Interessen.
ÜBER UNS
Kundenzufriedenheit jedes Mal.Gegenseitiges Vertrauen und gemeinsame Interessen.
Funktionstest.Die höchsten kostengünstigen Produkte und der beste Service sind unser ewiges Engagement.
Heißer Artikel
- Sind CR2032 und CR2016 austauschbar
- MOSFET: Definition, Arbeitsprinzip und Auswahl
- Relaisinstallation und Test, Interpretation von Relaisschaltplanen
- CR2016 gegen CR2032 Was ist der Unterschied?
- NPN vs. PNP: Was ist der Unterschied?
- ESP32 VS STM32: Welcher Mikrocontroller ist besser für Sie?
- LM358 Doppeler Betriebsverstärker umfassender Anleitung: Pinouts, Schaltpläne, Äquivalente, nützliche Beispiele
- CR2032 gegen DL2032 gegen CR2025 Vergleichshandbuch
- Verständnis der Unterschiede ESP32- und ESP32-S3-technischer und Leistungsanalyse
- Detaillierte Analyse der RC -Serienschaltung
 Eingehende Analyse von 1N4148 Dioden: Betriebsmodi, Spezifikationen und Nutzungsszenarien
Eingehende Analyse von 1N4148 Dioden: Betriebsmodi, Spezifikationen und Nutzungsszenarien
2024-05-08
 Verständnis der Typen und Verwendungen dynamischer und positiver Verschiebungspumpen
Verständnis der Typen und Verwendungen dynamischer und positiver Verschiebungspumpen
2024-05-07
Heiße Teilenummer
 CGJ5C2C0G1H103J060AA
CGJ5C2C0G1H103J060AA SMK325B7223KNHT
SMK325B7223KNHT GRM022R60J153ME15L
GRM022R60J153ME15L GRM1555C1H5R3WA01D
GRM1555C1H5R3WA01D 12105C105K4Z2A
12105C105K4Z2A GRM0336S1HR70BD01D
GRM0336S1HR70BD01D GRM1885C2A2R7CZ01D
GRM1885C2A2R7CZ01D F971V475KCC
F971V475KCC TAP224K050HSB
TAP224K050HSB EL7457CU-T13
EL7457CU-T13
- ISL8105IBZ
- VI-JW0-CZ/S
- STPS15H100CB-TR
- ADG1421BRMZ
- T491C225K035ZTZ012
- T491D156M035AT4380
- AD8226ARMZ-R7
- BQ4050RSMR
- MC74VHC245DTR2G
- T491A225M010ZTZ081
- ADP2380AREZ
- LMV339IDT
- STM32F217IEH6
- T491A335M016AT4513
- CD4013BPW
- BQ4802LYPW
- SN74FB2033ARC
- 215R7TZBKA12
- G5V-2-H1-12VDC
- ICS9FG104EGILF
- LB1638MTE-L
- NQ80000PH
- NX3DV221GM
- OR3T1256PS240-DB
- PCF8578T
- PT6302LQ-007
- TB31214FN
- TD62786AF
- TMPR28051-3-SL5-DB
- USS725D-DB
- W20395AA
- XC2S200E-6FTG256C
- AS7C256A-12JC
- C328A068PZQR
- NJG1600KB2
- WTR1625L
- CXD4950GG-W-T6
- RC2512FK-7W10RL
- SML-D12W8WT86AAD